简易算法原理与实现手册
排序算法
快速排序
快速排序定义了 Pivot 中枢值,每次排序的目标是(下文均以升序为例),希望排序后的 Pivot 值位置的左区间都比 Pivot 值小,右区间都比 Pivot 值大,也就是希望排序后,Pivot 值位置是正确的,且左右区间都对 Pivot 值偏序。
因此在递归树中,每层能绕过扫描的数据是树上层确定位置的 Pivots 集合。当 Pivot 每次都选择在中位数上,每层分别确定出 1、2、4、8 .. 个 Pivots,递归树近乎完全二叉树,其高度 $\log{n}$,从第 $i=1$ 层开始(第 0 层需要比较所有选出第一个 Pivot),每层只需要比较 $n-2^{i-1}$,为最标准情况;而当 Pivot 都选择为最值时候,每层只能选出一个 Pivot,递归树的高度为 $n$,每层需要比较 $n-i$ 次,总比较次数为 $\frac{n*(n-1)}{2}$。
比较便捷的实现方法是,先定下 Pivot 值,然后左往右扫描出不满足比 Pivot 小、右往左不满足比 Pivot 大的,交换这两个值,但在最后可能会存在匹配不到情况,比如下面代码的左边扫描越过了(忽略了)等于 Pivot 值的,这可能导致右边界的比 Pivot 小的值,无法与左边比 Pivot 大的进行交换,也无法与等于 Pivot 的进行交换,因此需要格外交换 Pivot 与右边界。
void qsort(vector<int>& arr, int S, int T) {
int P = S, L = S, R = T;
while (L < R) {
while (arr[R] > arr[P] && R >= S) R--;
while (arr[L] <= arr[P] && L < T) L++;
if (L < R) swap(arr[L], arr[R]);
}
swap(arr[P], arr[R]);
if (S < R - 1) qsort(arr, S, R - 1);
if (L < T) qsort(arr, L, T);
}
二路快速排序在相同元素的序列上,是需要 $n^2$ 的复杂度,三路快速排序应运而生,便捷实现,
void qsort(vector<int>& arr, int S, int T) {
int C = rand() % (T - S);
int P = S, L = S, R = T, E = 0;
swap(arr[P], arr[P + C]); // Pivot 选择随机化
while (L < R) {
while (arr[R] > arr[P] && R >= S) {
R--;
}
while (arr[L] <= arr[P] && L < T) {
L++;
if (arr[L] == arr[P]) {
swap(arr[++E + P], arr[L]); // 把相同的移到起始位置
}
}
if (L < R) swap(arr[L], arr[R]);
}
for (int i = 0; i <= E; i++)
swap(arr[R - i], arr[P + i]); // 把相同的又挪回来
R -= E;
if (S < R - 1) qsort(arr, S, R - 1);
if (L < T) qsort(arr, L, T);
}
基数排序
便捷实现,
void rsort(vector<int>& arr) {
vector<int> cnt(10);
vector<int> tmp(arr.size());
int maxVal = *max_element(arr.begin(), arr.end());
for (int k = 1; k <= maxVal; k *= 10) {
fill(cnt.begin(), cnt.end(), 0);
for (auto& i : arr) {
int d = (i / k) % 10;
cnt[d]++;
}
// 求前缀和得出 ID 分配数组
for (int i = 1; i < cnt.size(); i++) {
cnt[i] += cnt[i - 1];
}
// 从大到小分配(因为 ID 分配也是从高到低)
for (int i = arr.size() - 1; i >= 0; i--) {
int d = (arr[i] / k) % 10;
tmp[--cnt[d]] = arr[i];
}
copy(tmp.begin(), tmp.end(), arr.begin());
}
}杂类算法
全排列构造
一般都直接用 STL,如果需要手写,可以通过理解其含义手动实现。
- 假设有 $[1, 2, 3, 4, 5]$,满足单调连续递增,将其定义为全排列中第 1 个排列。
(当然数据不一定严格连续的,经过离散化后的连续也一样) - 并定义 $[2, 5, 4, 3, 1]$ 为第 $2 * A_{4}^{4} = 48$ 个排列。
(第一次,$A_{4}^{4} = 24$ 把 $[1, 2, 3, 4, 5]$ 后面的 4 位全部翻转,即变成 $[1, 5, 4, 3, 2]$ )
(那么,接下来 $[1, 5, 4, 3, 2]$ 的下一个全排列就是 $[2, 1, 3, 4, 5]$ ,即第 25 个排列)
(第二次,$A_{4}^{4} = 24$ 把 $[2, 1, 3, 4, 5]$ 后面的 4 位全部翻转,即变成 $[2, 5, 4, 3, 1]$ )
当面临计算 $[2, 5, 4, 3, 1]$ 的下一个排列时,我们可以手动计算出是 $[3, 1, 2, 4, 5]$,这是因为我们知道后面 4 位($[5, 4, 3, 1]$)是逆序了,也就是已知其经历了 $A_{4}^{4}$ 所有排列,所以,下一个排列的倒数第 4+1=5 位(即顺数第一位)要变成后面 4 位中的数值 3。
对应代码中就是,
- 从后往前寻找第一个非逆序,由于 2 < 5,数值 2 是非逆序的起点,记录下标 p = 0;
- 从后往前寻找第一个大于数值 2 的值,对应 3 > 2,记录下标 q = 3;
- 交换,此时得到 $[3, 5, 4, 2, 1]$,此时,观察可得,后面四位其实是 $[3, 1, 2, 4, 5]$ 经历 $A_{4}^{4}$ 排列后的结果,只需要反转 [p + 1, R] 区间即可;
- 同理,当找不到第一个非逆序时,也就是对应 $[5, 4, 3, 2, 1]$,只需要反转,即可复原。
bool reverse(int arr[], int L, int R) {
for (; L < R; L++, R--)
swap(arr[L], arr[R]);
}
bool next_permutation(int arr[], int L, int R) {
if (L == R) return false;
int p = R, q;
for (;;) {
p--;
if (arr[p] < arr[p + 1]) { // 1. 寻找第一个非逆序
q = R;
while (!(arr[p] < arr[q])) q--; // 2. 寻找第一个大于 arr[p] 的值
swap(arr[p], arr[q]);
reverse(arr, p + 1, R);
return true;
}
if (p == L) {
reverse(arr, L, R); // 4. 复原全排序
return false;
}
}
}二叉树还原
通过先序或后序特性确定根,然后中序确定左右子树,从而确定子树的根,递归还原出二叉树。
为什么已知先序和后序不能确定一棵二叉树呢?因为假使我们确定了根,但是左右有一位置为空,在根左右(先序)和左右根(后序)的信息下,无法确定空的结点是左边还是右边。
树型结构
二叉堆
以大顶堆为例,维护根结点大于等于左右孩子结点的特性。
- 入队,插入到堆尾,然后将父结点与其比较,向上冒泡排序调整。
- 出队,返回根,用堆尾覆盖根,挑左右孩子结点中最大的与其比较,向下冒泡排序调整。
AVL 树
AVL 树实现方法有两种,一种是直接记录子树高度,另一种是记录 EH、RH、LH、LE、RE 的平衡因子的,可参考:平衡二叉树(AVL)的创建、插入、删除。由于树高直接记录高度,而平衡因子只记录相邻子树关系,删除后子树树高可能不只相差1个高度,所以引入 LE、RE 平衡因子,实现因此略复杂,但性能要比记录树高的要好很多。
B/B+ 树
B 树的数据会记录在中间结点。除根外需要保证大于等于有 $N/2$ 个子结点。
其中 $N$ 阶(也称之为度,与图论的出度,即点出发的边数含义一样,或者 Fanout)表示最多有 $N$ 个子结点,$N – 1$ 个关键字。
插入只有 SplitChild() 横行扩展兄弟结点;删除分两种,在叶子结点直接移除,在非叶子结点删除找到前驱或者后继结点替换,然后回溯时候,观察操作的子树是否满足最小度(不满足则破坏了 B 树结构),其调整方式分为相邻兄弟结点借用(借用后可满足最小度)或合并(借用不满足最小度,只能把相邻兄弟及值相邻的父结点的一个关键字合并)。
B+ 树的数据只记录在叶子结点,非叶子结点的记录索引。
插入同样的 SplitChild() 横行扩展兄弟结点;删除只有在叶子结点,回溯借用相邻的关键字,或者合并,然后回溯的处理与 B 树对回溯的处理类似,首先更新结点索引的关键字是否与被删的一致,是则重新计算该位置的索引关键字(基本实现是左子树的最大值),然后还是借用或者合并,借用是直接借用相邻的子树,然后对于相关的索引关键字直接重新计算(本质上有部分是必须计算得到的,比如在末尾借用右子树后,其本身无记录关键字,需要计算得到)。
C++ 简单版的 B 树与 B+ 树的实现可在参考资料中获取。
红黑树
2-3-4 树(4 阶 B 树)演变,红色代表边缘关键字,黑色代表中间关键字,一个 2-3-4 树整体结点对应红黑树的一个黑色结点,同构的结构,使得红黑树的所有树枝经过的黑色结点数一致。插入可以按照 2-3-4 树模拟,但删除不能用同构方式,把 2-3-4 树删除直接搬过来,而是依赖性质(或者依赖维基百科)。
插入
新创建的插入结点(Now Node 以下简称 N)是红色,插入矛盾的情况只有:父结点(Parent,以下简称 P)是红色的。
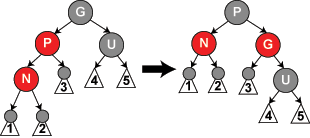
插入到 4 结点(P 红色、祖父结点,Grandpa Node 以下简称 G,必然黑色
观察叔叔结点(Uncle Node,以下简称 U),如果也是红色的,说明 P、G、U 组成完整的 4 结点,如同 B 树的分裂,G 的关键字被添加到曾祖父的结点旁边,也就是 G 变成红色(递归回溯的时候等同于新插入结点)P、U 变黑色,完成分裂;
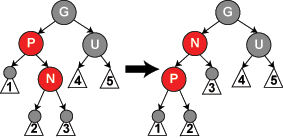
插入到 3 结点(P 红色、G 必然黑色)
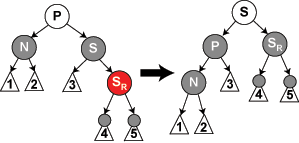
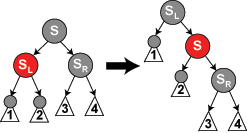
观察 U,如果是黑色,说明 P、G 组成 3 结点,此时结点还没满,显然不能插入的原因是,之前标记的代表中间关键字的黑色 G,已经不合时宜了,通过能保持同构的旋转使它们组成 4 结点(左旋右旋本质并不破坏二叉树的有序性,另 ,红黑树旋转同时要保留颜色,不保留就会导致不能同构的旋转);比如 N < P < G,当然需要选择 P 作为黑色中间关键字结点,然后 N、G 红色,组成 4 结点(如图一);比如 P < N < G,那就是需要选择 N 作为黑色中间关键字结点;至于旋转方式,如 P < N < G,先 N 左旋(图二),再 N 右旋(图一,图中的 P 即图二的 N)。更详细可参考:维基百科红黑树插入。
删除
红黑树的删除,旋转不超过三次,而 AVL 最坏情况旋转到根(删除与旋转调整导致子树高度下降,引发连锁不平衡),更多参考:关于AVL树和红黑树的一点看法。黑色叶子结点的删除是平衡修复的难点,因其删除可能带来整颗树的黑色树高 -1;因此,修复函数的含义是使不涉及删除的子树满足平衡;另外,修复其实有很多方法,但好的方法是优先于减少红色结点,因为树链中红色结点越多,相较于同样平衡的只有黑色结点的树链,其查找深度越深,所有平衡操作首先确定能平衡且能尽量减少红色结点的情况。下面以左子树的删除为例讨论(和维基百科的红黑树删除一样)。
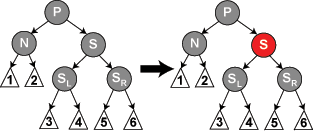
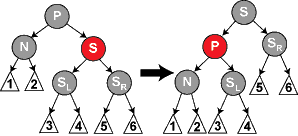
N 表示包含已删除黑色结点的子树,即,N 下的黑色树高 -1。在下图情况,其 S(Sibling Node,兄弟结点)标记为红色即可,因为 SL、SR 是黑色的。但此情况不是平衡情况,只有经过 P 的树链黑色树高 -1,其他树链不变,所以需要回溯到 P 上,对 P 的兄弟子树执行修复操作,操作可能直至根。
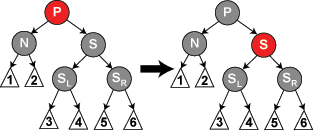
同理,交换 P 与 S 的颜色。此情况是平衡情况,P 的子树黑色树高并无增加或减少,无需继续修复,直接返回即可。
重点情况。S 左旋,SR 转黑色。此情况也是平衡情况,无需继续修复。
这是服务于重点情况,当 SR 是黑色的时候,通过旋转得到红色的 SR。
最后一种情况,当 S 是红色,可通过旋转,把状态转移到上面几种情况。
图结构
Dijkstra Shortest Path
- 建立红点集,定义点集内任意点与起点的路径为最短路。
- 由红点集内出发松弛蓝点集中路径最短的点,由此扩充红点集。
(松弛过程,也就是更新红点集与蓝点集之间距离)
(过程可用优先队列,出队的第一个就是路径最短的点) - 由于红点集的扩充,最终将覆盖整个图,于是求出起点与任意点的最短路。
同理,最小生成树的 Prim 算法,只是红点集意义变成使点集内任意两点为最短距离。
Floyd Shortest Path
- 求传递闭包,或者多源最短路查询。
字符串结构
KMP 匹配
- 定义模式串循环节的 next 数组:$$next[i+1]=1+k \ ,条件是 \ str[1..k] == str[i-k+1..i]$$这意味着在第 $i+1$ 位置,一旦该位置不相等,但是前面长度为 $k$ 的数据,与模式串开头到长度为 $k$ 的段落一致,即已成功匹配,因而可从 $k+1$ 开始比较。
(长度是理解的 next 数组的桥梁) - 进行匹配时,过程中遇到不相等的地方让模式串后退到上一个循环节,即 $next[j]$,然后再比较。
- 在计算 next 数组时,也可以利用 next 数组的特性,即在 $j$ 位置,已知 $next[j-1] = 1+k$,如果在 $j$ 位置上与 $next[j-1]$ 位置的字符一致,则 $next[j]=next[j-1]+1$,也就是对长度 $k$ 加一位,反之往前跳跃。
TODO: DP..,Dinic 最大流,最小费用最大流,后缀数组,AC 自动机,计算几何,K-D 树,联通
参考资料
- 本文实现的 B/B+ 树:https://nlogn.art/wp-content/uploads/2021/04/BTree_BPlusTree.zip
- 本文实现的红黑树:https://nlogn.art/wp-content/uploads/2021/04/RBTree.zip
- 演算法筆記:http://www.csie.ntnu.edu.tw/~u91029/index.html
- 演算法筆記(新地址):http://web.ntnu.edu.tw/~algo/
- ACM 模板:https://github.com/axiomofchoice-hjt/ACM-axiomofchoice
- OI-WIKI:https://oi-wiki.org/